The recent successes of SpaceX, Blue Origin, and other companies have made it clear that the space industry is undergoing dramatic change. After decades of a centralized approach to achieving primarily public-sector priorities, a new decentralized pursuit of private-sector goals has renewed faded dreams of expansive—commercially driven—human activities in space. Space tourism, manufacturing, resource use, and even colonization are again on the minds of space enthusiasts and, more important for our purposes, businesspeople.
To fulfill the promise of this commercial space revolution, the industry has to overcome substantial obstacles. Space is hard, as the saying goes, and the business case for making the large initial investments required to dramatically expand human activities in space is far from clear. Some skeptics believe the current surge of enthusiasm for space is mostly hype and will end up producing few lasting, substantial changes, at least unless we discover creative ways to overcome these challenges.
One challenge facing the industry is the interdependence of many space companies’ business models. For example, if launch costs fall, space manufacturing becomes more feasible, which in turn creates demand for more space launches, further driving down costs and creating a virtuous cycle. Economists call these feedback effects “complementarities,” and they are a double-edged sword. In particular, complementarities left unrealized can leave an industry trapped in a state of underdevelopment, where no party acting alone benefits enough to get the virtuous cycle started.
Economists have captured the problem of complementarities through a memorable game called the Stag Hunt. In the Stag Hunt game, there are two hunters, A and B. Each hunter chooses whether to hunt a hare or a stag. Hares can be hunted individually, while stags must be hunted together, and stags are worth much more than hares to the hunters. Figure 1 shows how this game is typically represented, with hunter A’s choices in the rows and hunter B’s choices in the columns. Within each cell, the first number represents the payoff to A and the second number the payoff to B. To connect this game to commercial space, you might imagine which activities in space better fit under the categories of hares—modest and unilaterally achievable—and stags—big, bold and necessarily team efforts.
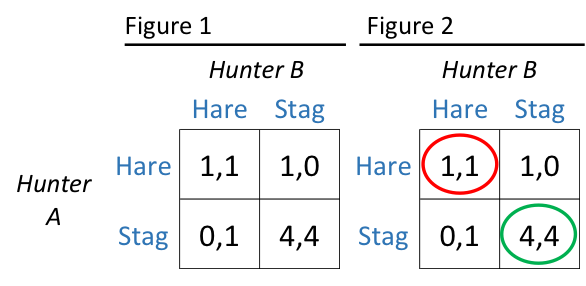
Figure 2 shows the equilibria of the Stag Hunt game. To find them, consider the strategies each hunter should adopt given the other hunter’s play. Suppose hunter A expects hunter B to hunt the hare: then it will be better for A to hunt a hare (and earn 1) than to hunt a stag (and earn 0). The same logic holds for hunter B, so one equilibrium of the game is for both A and B to hunt the hare, as outlined in red in the figure. But now suppose that hunter A expects hunter B to hunt the stag. Then it will be better for A to hunt the stag (and earn 4) than to hunt the hare (and earn 1), and the same logic holds for hunter B. Therefore, a second equilibrium holds in which both A and B hunt the stag, outlined in green in the figure, and this equilibrium is substantially better for each of the hunters.
The power of the Stag Hunt game is to capture the all-too-common situation in which complementarities not rewarded by the market can leave an industry (or a society) stuck in an inferior equilibrium. Everyone in the Stag Hunt would agree that cooperatively hunting the stag is a superior equilibrium, but no individual has the incentive to unilaterally pursue a stag once the players find themselves hunting hares. To see this explicitly, note that starting from the upper left corner of Figure 2, either individual would lose by unilaterally pursuing the stag.
Economists have identified at least two ways to overcome this risk in the Stag Hunt: public (or private) intervention in the payoff structure, and private coordination through reputation and repeated play of the game. Both of these strategies are directly relevant to the commercial space revolution.
For example, consider what a government (or large investor) might do to change incentives. It might subsidize (fund) unsuccessful stag hunting and tax (retain a share of the returns to) successful stag hunting, producing payoffs like those shown in Figure 3. In this situation, the only equilibrium is to hunt the stag together. Everyone wins, because the government (or large investor) has used its tools to manage the complementarities. In the context of space, some of the current efforts of commercial space companies can be thought of as hares, with the bigger, bolder visions—the stags—left unpursued.
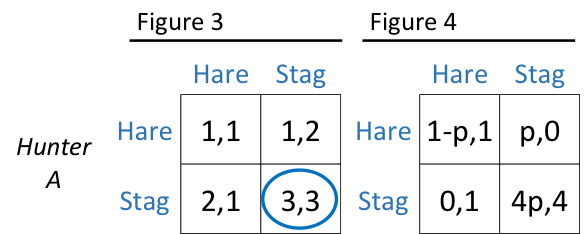
An alternative solution to the Stag Hunt is for reputation and repeated play to support cooperation. Suppose, starting from a hare-hunting equilibrium, hunter A unilaterally announces that he will hunt a stag. If this announcement is believed by hunter B with probability p, hunter A will find it better to abide by his announcement and hunt the stag whenever p>0.25 (see Figure 4). How can such trust be established? By repeated play and the building up of credibility. In space, where the players are few and the key decision-makers even fewer, establishing such reputations should be a promising way forward.
The current revolution in commercial space holds out the promise of civilizational impact. For the first time in history, we may have the collective opportunity to design societies nearly from scratch and to make humans a multi-planetary species. But to make such a possibility a reality, the interdependencies between the drivers of the commercial space revolution must be captured and converted from obstacles into incentives.
